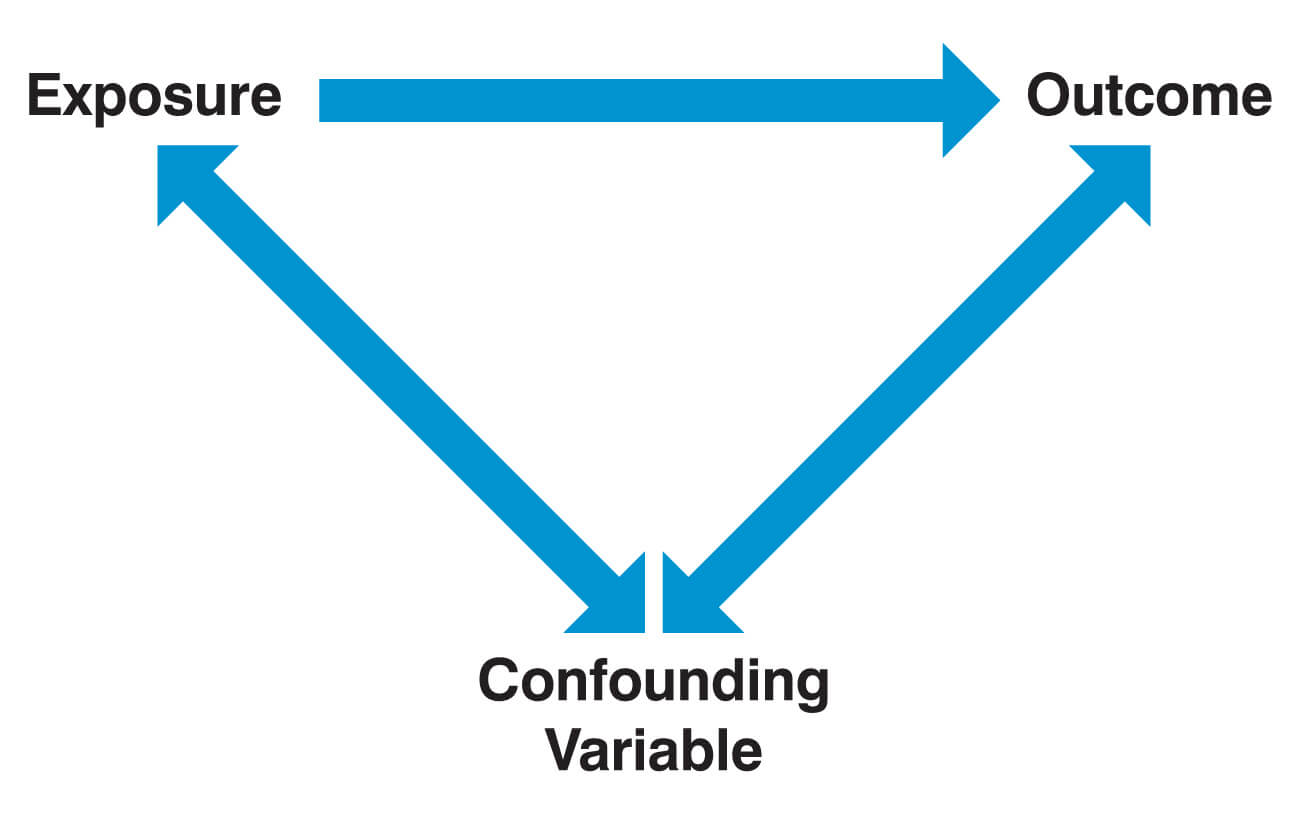
Confounding factors
A confounding factor is a variable that is associated with both the outcome of interest and the exposure of interest. In this constellation, the exposure of interest appears (spuriously) to be associated with the outcome of interest, while in reality, it is the confounding factor (the “third variable”) that causally affects the outcome. Importantly, a variable is not considered a confounder if it lies on the causal pathway between the exposure of interest and the outcome.
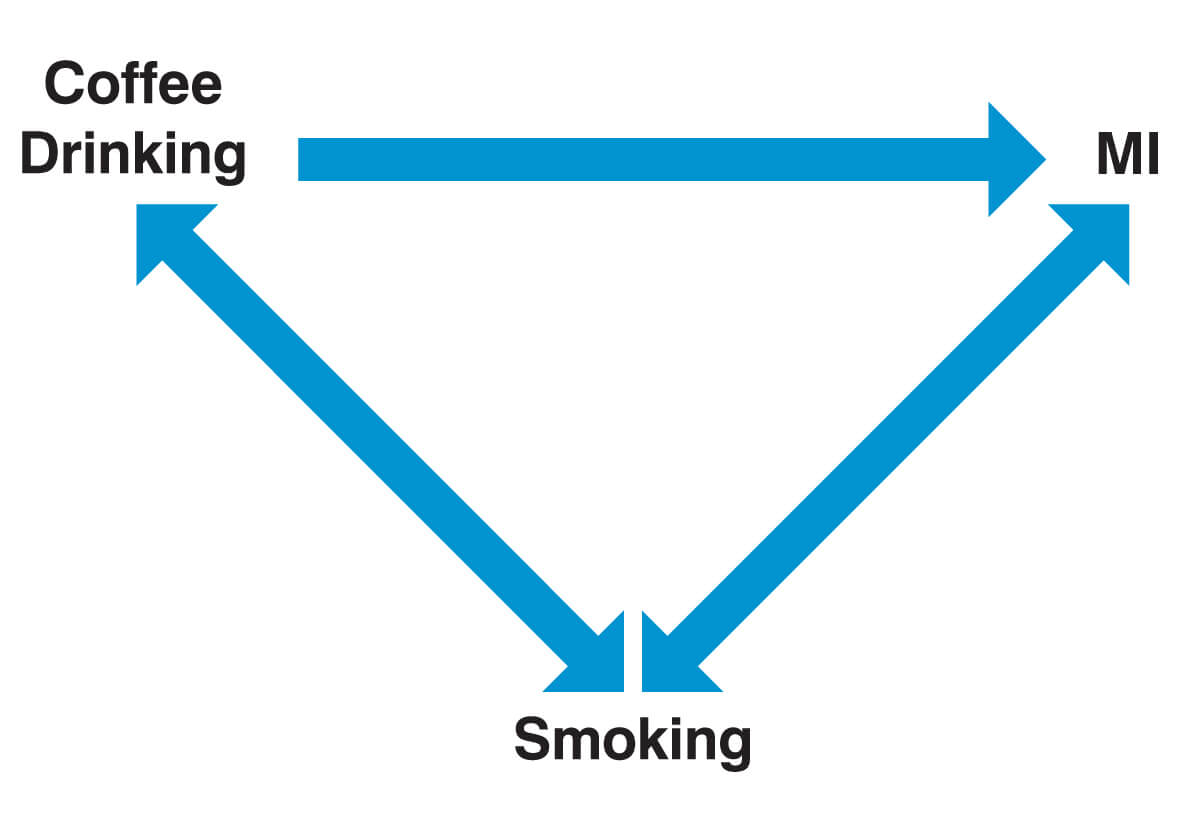
A commonly quoted example of a study that has a confounding variable is one that established a link between coffee consumption and myocardial infarction (MI). Coffee drinkers were indeed found to have an increased risk of suffering a MI. The confounding factor, in this case, is that coffee drinkers also smoke more significantly and that the increased risk of MI is actually attributable to this.
Confounding can result in:
- The observation of a difference between study populations when one does not exist
- The failure to observe a difference between study populations when one actually exists
- The underestimation of an effect
- The overestimation of an effect
Confounding factors need to be accounted for by the researcher. There are two commonly applied ways to do this:
- Stratification: In the example of the coffee drinker study, participants are grouped into two groups, smokers and non-smokers. The risk ratio associated with coffee drinking is then calculated within each group separately and then pooled. The resulting pooled risk ratio is then “adjusted (or controlled) for” smoking.
- Multivariable regression analysis: This is a more complex approach that uses statistical models (e.g. logistic regression for binary outcomes, linear regression for quantitative outcomes or Cox-regression for survival data) to adjust for confounders. In contrast to stratification, the regression approach allows adjusting (or controlling) for multiple confounders at the same time.
Distinguishing between causal and non-causal associations may be difficult. For example, if one were to study the effect of hypertension on the risk of stroke, should one adjust for diabetes, which may be both causally and non-causally related to hypertension? To help with such decisions, researchers increasingly make use of directed acyclic graphs (DAG) to guide the statistical modelling approach.
Bias
Bias is a systematic error in how a trial is designed or run, resulting in an inaccuracy in the result. While confounding is a problem due to particular characteristics of the study population, bias is a problem due to the study design itself. Confounding can be eliminated by randomisation, which balances all potential confounders equally among groups. In contrast, randomisation is usually of little help in the avoidance of bias.
There are numerous types of bias that can occur at various stages of the study process. Most forms of bias can be grouped as follows
- Selection bias
- Performance bias
- Measurement bias
- Publication bias
Selection bias
Selection bias occurs when the groups compared differ systematically in the way participants were enrolled into the study or dropped out from the study. For example, selection bias commonly occurs in case-control studies if controls are selected that come from a different source population than the cases (e.g. they would not have come to that hospital had they fallen ill with the same disease). In a randomised controlled trial comparing a drug (e.g. ACE inhibitor) against placebo, more people in the drug arm may drop out of the study because they experience side effects of the treatment (e.g. cough due to the ACE inhibitor). Dropping out of a study is commonly associated with lower socioeconomic status, which, in turn, is associated with poor health outcomes. Selection bias, in this case, gives the spurious impression that the drug is effective. Because of side effects, high-risk individuals are more likely to drop out from the active arm than from the control arm. This is sometimes called attrition bias.
Neyman bias (prevalence-incidence bias) is a specific form of selection bias that occurs in case-control studies when the prevalence of a condition does not reflect its incidence. For example, if a disease is characterised by early fatalities and a significant period of time has elapsed between exposure and case selection, the ‘worst cases’ may have already died.
Berkson bias (admission bias) is another example of selection bias that occurs when the hospital admission rate of controls and cases are different from one another because the combination of exposure to risk and occurrence of disease increases the likelihood of being admitted to hospital. This produces a systematically higher exposure rate amongst hospital patients and distorts the odds ratio.
Another example of selection bias is diagnostic purity bias. This occurs when patients with a co-morbidity are excluded from a study. In these circumstances, the sample will no longer reflect the true complexity of the population.
Performance bias
Performance bias occurs when systematic differences exist between the care provided to the different intervention groups in the study that is actually part of the treatment of interest. The observed effect of a certain treatment may be spurious. In reality, it may be the increased attention given to patients in the treatment arm that improves their outcome.
Measurement bias
Measurement bias occurs when the way that an outcome is assessed produces systematically different results in the two groups compared. Often, it is the knowledge by the patient (the responder) or the researcher (the observer) of the group to which a patient is allocated that leads to measurement bias. Measurement bias is therefore often subdivided into observer and responder bias.
Observer bias occurs when knowledge of treatment allocation causes an ‘observer’ of the research (i.e. the research team) to fail to properly or impartially measure the outcomes correctly.
Responder bias occurs when knowledge of group allocation changes the behaviour of a patient or the way he responds to questions. A common form of responder bias is recall bias, where participants are aware of their treatment or exposure status and therefore knowingly or unknowingly alter their response to questions asked by the observer. For example, the anxiety experienced by cancer patients may cause them to more acutely remember past episodes of radiation exposure (e.g. X-ray) than control individuals without cancer. Another example is when an intervention aimed at smoking cessation may cause smokers in the intervention arm to lie about their current smoking status for fear of being seen as non-compliant with the intervention. Control individuals who did not receive the smoking cessation intervention may more often correctly report their current smoking status.
The Hawthorne effect, also known as the observer effect, refers to a phenomenon by which people alter or modify their behaviour, usually in a positive manner, due to the fact that they are being observed in a research study. The Hawthorne effect, however, only leads to bias if the change in behaviour due to being observed differs across the groups compared in a study. Then it is similar to performance bias except that it is not the staff involved in the treatment of patients but the patients themselves who alter their behaviour.
Publication bias
Publication bias occurs when the results of published studies are systematically different from the results of unpublished studies. In these circumstances, reviewers are in danger of drawing the wrong conclusion about what the body of research shows. This can potentially have dangerous consequences for patients.
A well-known example of this was the withdrawal of the anti-inflammatory drug Vioxx (rofecoxib) due to safety concerns by its producer Merck. Media reports accused Merck of having prevented the publication of studies that indicated a high prevalence of cardiovascular events in patients taking Vioxx long-term. If this was true and this data had been published, a different conclusion about the safety of Vioxx may have been drawn at an earlier stage.
Effect modification
Effect modification (interaction) occurs if the effect of a risk factor on an outcome measure differs between different levels of a third variable (for example, gender, ethnicity or smoking status). Smoking status is a common effect modifier. A classic but somewhat controversial example concerns the finding that asbestos exposure may disproportionally increase the risk of lung cancer in those exposed to asbestos that are also smokers. Asbestos exposure alone increases the risk of lung cancer threefold, which is a risk ratio of 3. Smoking alone is thought to increase the risk of lung cancer tenfold (risk ratio of 10). In the absence of effect modification, we would expect that those exposed to both asbestos and smoking to have 30 times higher risk (3 x 10) of lung cancer than those who don’t smoke and are not exposed to asbestos. However, some (but not all studies) have suggested that the risk associated with the combined exposure (smoking and asbestos) compared to those exposed to neither is much higher than 30 and may be as high as 60. The effects of smoking and asbestos exposure have combined to have a multiplicative effect. Asbestos and smoking are then said to be interacting because the combined effect is greater than one would expect.
It should be noted that it would still be called an effect modification or interaction if the combined effect were smaller than expected, for example, if the risk of lung cancer due to asbestos exposure were smaller in smokers than in non-smokers.
In rare cases, effect modification can even lead to a factor being a risk factor in some people (e.g. women), but a protective factor in others (e.g. men). On average, these two effects would cancel out, and we would see no effect in the total population.
Unlike confounding, effect modification is a biological phenomenon in which the exposure has a different impact in different circumstances, which may be of scientific interest. Often, however, one will find evidence for differences in effects among various subgroups by chance alone. Unless there is a good biological reason to suspect effect modification, differences in effects among groups are likely to be due to chance and should not be given too much importance until a further study has confirmed the finding.
Header image used on licence from Shutterstock
Medical Exam Prep would like to thank Dr. Marc Barton for permission to reproduce this extract from his book ‘Evidence-Based Medicine & Statistics for Medical Exams’.
About Dr. Marc Barton
Dr. Marc Barton qualified from Imperial College School of Medicine in 2001. Since that time he has worked in a variety of different medical specialities. He worked as a GP partner from 2006 until 2008 and more recently as a higher specialist trainee in Emergency Medicine.
‘Evidence-Based Medicine & Statistics for Medical Exams’ is available for purchase here.






